Fondamentaux mathématiques en France, en cycles 1 et 2 : les deux voies d’apprentissage
1/ Préambule : La pensée et l’Image Technique dans les apprentissages des fondamentaux mathématiques
- Présentation théorique : un concept est une idée générale mais on peut en distinguer deux familles :
- La première est issue de notre pensée et s’appuie sur des exemples puisés dans notre environnement naturel. Piaget la nomme l’« abstraction empirique ». Ce qui la caractérise, c’est un mot de notre vocabulaire habituel que nous pouvons associer avec une « image technique ». Un cheval est représenté à la fois par un mot écrit du langage et par une image concrète, dite « technique », selon Vygotski (figure 1). Cette image première est unique, représentative et doit être proposée par le médiateur, l’enseignant. L’image d’un mouton ne sera pas proposée. Mais le « cheval », peu importe sa robe, est une image de cheval pour notre cerveau, comme une fleur, rose, lilas ou tulipe sera une image du concept « fleur ». On ne peut proposer plusieurs « images techniques ». En effet Johann Fahrenfort démontre en 2012, à l’IRM fonctionnel, que des images « premières » concurrentes, pour un même concept, sont effacées par le cerveau profond et donc « non visible par la conscience 1 ».
Après l’enregistrement dans le cerveau, la prise de conscience s’effectue et alors, ensuite seulement, des images secondaires pourront se greffer, sans aucune limite, à cette image technique principale ou première.
Figure 1 La pensée verbale selon Vygotski (1934)
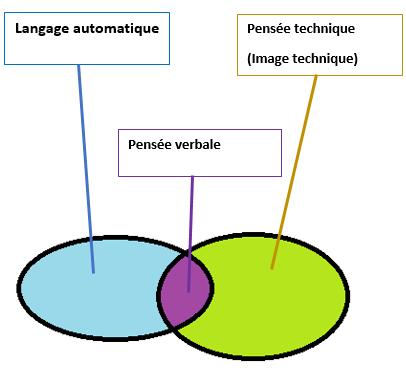
Cheval

Concept d’« Abstraction empirique »
1 Fahrenfort J, Snijder T, Heinen K, et coll. Neuronal integration in visual cortex elevates face category tuning to conscious face perception. PNAS 2012, 109 :21504-9 Saygin Z, Osher D, Koldewyn K, et coll. Anatomical connectivity patterns predict face selectivity in the fusiform gyrus. Nature Neuroscience 2012, 15 :321-7
b) La seconde est également issue de notre pensée, aussi, mais elle est construite par notre raisonnement sans avoir d’exemples concrets sous les yeux, par exemple « la Liberté », « la Philosophie ». On ne peut en définir une image technique, seulement proposer une définition formulée grâce à notre capacité de raisonner, pour en approcher le sens. Il n’y a pas de représentation mentale imagée première. Nous parlerons d’« abstraction pure ». Un symbole peut être utilisé pour représenter ce concept, par exemple, la lettre grecque φ pour la Philosophie. Ce symbole représente la Philosophie, conventionnellement mais ne dit rien sur le sens de « la Philosophie », dont une définition pourrait être « La Recherche de la Vérité » ou « Réflexions devant conduire à la Sagesse ».
-
En Mathématiques, nous parlerons plutôt de « Notion » que de concept. Pour rendre les mathématiques concrètes, nous allons accorder chaque notion avec une image technique. Or l’École de la République présente toutes les notions avec une définition, comme s’il s’agissait d’une abstraction pure et laisse le soin à l’élève de retenir une image parmi toutes celles proposées. Il les oubliera toutes.
-
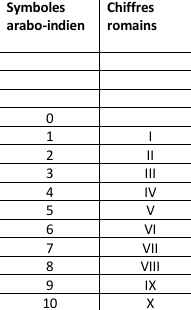
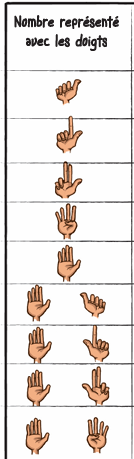
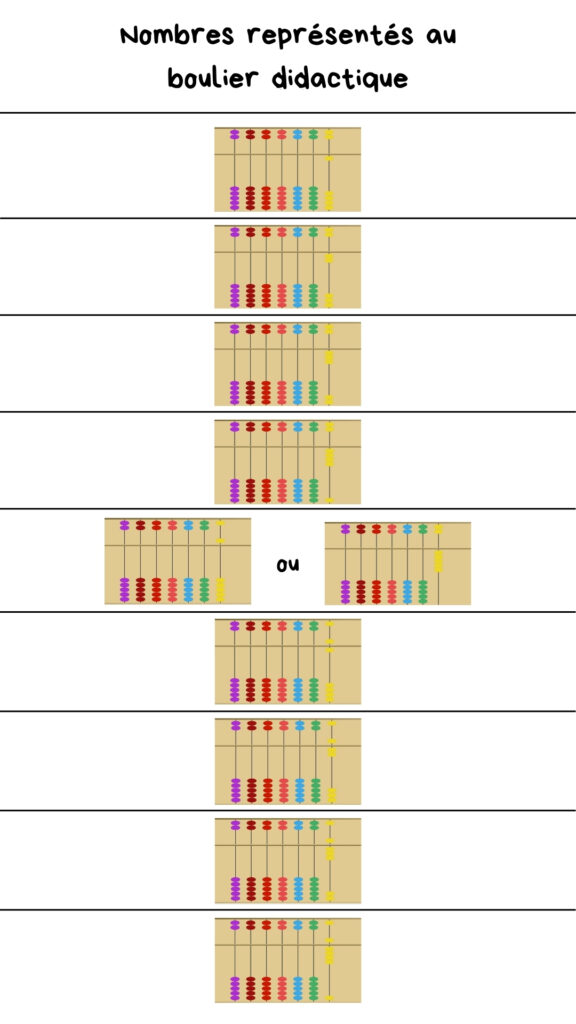
Les premières notions apprises sont celles des nombres entiers. Ils peuvent être représentés en chiffres arabes, en chiffres romains, avec les doigts des deux mains, figurés par des points sur un graphique, formulés en mots. Pour l’école, « huit », c’est le nombre correspondant au nombre sept auquel on ajoute un, ou le nombre auquel il faut ajouter deux pour obtenir dix (le complément à dix). Les nombres sont, alors, représentés, par le symbole indo-arabe qui ne dit rien sur la quantité. On ne propose pas d’image technique du nombre, si ce n’est une multiplicité d’images secondaires qui vont subir le sort décrit par Yohann Fahrenfort. Il ne viendrait à l’idée de personne de proposer pour un cheval, sous prétexte que c’est un mammifère, des images de mouton, de chien ou d’ornithorynque. C’est pourtant ce que l’on fait à l’école avec des dominos, les doigts arrangés de façon diverse ainsi que des constellations variées. Non, l’image technique de huit, ce n’est pas le domino 4 et 4, ou 6 et 2. L’image technique, c’est seulement l’image des doigts 2, avec une main et trois doigts ainsi que le complément 2 à 5 ou à 10. Les dominos ont des images secondaires. « Trop d’informations tuent l’information » selon l’adage. C’est le cas. Le nombre va, donc, rester abstrait pour beaucoup d’enfants et être représenté seulement par le symbole indo-arabe qui est une image symbolique et non technique, comme la lettre grecque φ pour la Philosophie. Le boulier didactique prolonge, lui, les mains en utilisant les mêmes images techniques pour toute la numération. C’est le « code analogique » demandé par l’ÉN en plus du « code arabe » dans le « Triple Code » (figure 2).
2 La Méthode des Abaques, p. 11, mars 2012
Le troisième code est le « code oral ». Sa construction, dans notre numération conventionnelle archaïque, et en Français seulement, est totalement irrégulière et illogique, comme déjà vu dans le système de Condorcet ou le système conventionnel . Dans ces conditions,
-
Aucune image technique ne pourra être mise en place, du fait des irrégularités (56) qui condamnent le reste (34 hors première dizaine) à être, de fait, irréguliers aussi.
-
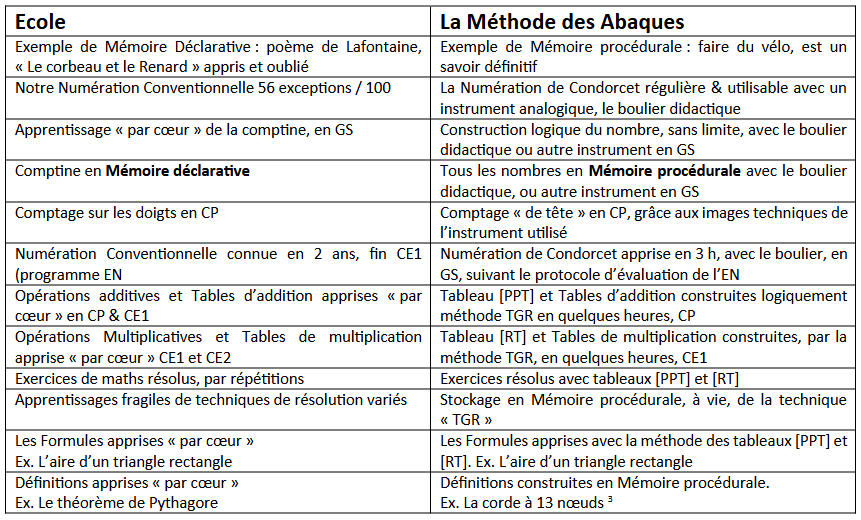
La mémoire procédurale ne pourra absolument pas s’activer et seule la mémoire déclarative le (par cœur) pourra être utilisée, aujourd’hui. Le processus toxique de l’École est enclenché (figure 3, colonne de gauche). On apprend tout par cœur, comme un poème, la logique n’est pas accessible. C’est la cause du retard de tous nos écoliers, d’au moins deux ans par rapport à l’étranger. Les classements internationaux Timss le mesurent depuis 10 ans, en CM1.
En l’absence de la logique du nombre, nous démontrons que ce processus mental s’engage pour tous les enfants de CP, c’est l’apprentissage par cœur des mathématiques, d’abord la comptine, ensuite les opérations, puis les tables d’addition et de multiplication, et enfin toutes les autres notions (théorèmes, formules, etc.). Pour le théorème de Pythagore, par exemple, un triangle rectangle ABC ou la formule a² = b² + c², ne sont pas des images techniques premières, ce sont des images secondaires au contraire de la corde à 13 nœuds qui est une image technique première.
Figure 3 Tableau des Fondamentaux mathématiques
2/ De la Numération, la mauvaise voie d’apprentissage, la Numération Conventionnelle Archaïque,
En Français, pour nommer les nombres de zéro à cent, plus d’une irrégularité sur deux expressions. On ne peut plus parler d’exceptions ; l’absence de logique est la règle et les origines de ces anomalies sont extravagantes ?
La première dizaine est issue du latin en ligne directe, à part « huit » qui est l’évolution de octo, vers oit (au XIIème siècle) qui a donné huit. Ces premiers nombres de 0 à 10 sont nommés (langage automatique écrit) par des mots empruntés au latin qui possèdent chacun une image technique (selon Vygotski), respectant la subitisation, avec des représentations grâce aux mains et aux doigts4 (figure 2) La notion mathématique (concept), nombre, est alors parfaitement décrite par un mot (langage automatique) et une image technique pour toute cette première dizaine.
La pire difficulté pour les enfants, commence dès la seconde dizaine :
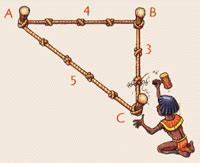
3 La corde à 13 nœuds
4 La Méthode des Abaques, p. 11, mars 2012,
En latin « decim » vient du sanskrit « dekem » ; « undecim » se traduit par un-dix, puis au cours du temps decim devenant « dece », puis « ze », le mot évolue vers onze, et toute la série, de même, vers douze, treize, quatorze, quinze, jusqu’à seize. Les nombres défilent sans aucun lien apparent pour un non-latiniste, avec dix. L’analogie avec un, deux, trois, etc. est aussi trop lointaine. On dit donc, en fait, sans comprendre, l’équivalent d’un-dix, deux-dix, trois-dix, quatre-dix, cinq-dix, six-dix. Et ensuite, que se passe-t-il ? La numération romaine est une numération additive et pour éviter le trop grand nombre de caractères, les « latins » avaient pris l’habitude de représenter l’écart, à cinq, à dix ou à la dizaine, soit IV au lieu du IIII Étrusque, IX au lieu de VIIII et on disait couramment « duodeviginti », soit « vingt moins deux » (écart de deux à vingt). On aurait pu écrire, au lieu de XVIII, « XIIX » mais écrire en toutes lettres « vingt moins trois », « vingt moins deux », « vingt moins un », ce n’était pas possible en Français dans le cadre de la numération positionnelle. On a donc repris la liste précédente, de façon moderne mais en changeant le sens dix-sept au lieu de septze, dix-huit, au lieu de huitze, dix-neuf au lieu de neufze. Pourquoi cette rupture à dix-sept et l’adoption ici du vrai sens d’écriture, sept après dix et des bons morphèmes, sept et dix, du nombre écrit ? Il ne faut pas chercher très loin, c’était la langue de la rue, irréfléchie et approximative ; les lettrés, eux, parlaient le bon latin de Cicéron et n’étaient pas concernés par les dérives de la langue du peuple. Pensez-vous que les enfants devant cette série de nombres, inintelligibles au début avec le morphème -ze qui permet la construction, et finalement avec le morphème dix, ne soient pas perturbés, dubitatifs, perplexes ? Leur cerveau ne peut qu’apprendre par cœur, en changeant de morphème au passage, d’abord dans un sens puis dans l’autre, la modification de l’un à l’autre se faisant de façon arbitraire et incohérente, à partir du sixième rang. C’est une irrégularité majeure et déstabilisante. Le rappel de « dix » et du rang de la suite ordonnée arrive enfin, pour trois nombres seulement, dix-sept, dix-huit et dix-neuf. Leur cerveau d’enfant est, assurément, gravement perturbé dans cette approche des maths qu’on leur annonce comme « logique » ?
Ensuite, où est la logique dans vingt ? C’est du « bas Latin », vinti au lieu de viginti, (Vème siècle) ; de même pour trinta qui a donné trente, dérivé du latin populaire (Xème siècle), alors que toutes les autres dizaines jusqu’à soixante dérivent du suffixe « -aginta » (langues indo-européennes et sanskrit) pour donner le suffixe ante dans quarante, cinquante, soixante. Même pour trente il faut écrire « trante » avec un « a ». Nous ne devons pas maintenir une seule exception, qui perturberait la logique. Condorcet n’avait pas osé faire ce changement, nous le faisons !
Enfin, les cerises sur le gâteau ! Les restes du système gaulois de numération sont alors utilisés pour la suite de la construction dans le système vigésimal, ou vicésimal, Celte ou gaulois (en base vingt). Les milieux populaires ne savaient compter que jusqu’à soixante, dans le système sexagésimal, utilisé pour les calculs de durée en minutes, heures, jours, mois … Compter jusqu’à soixante suffisait pour dénombrer les quantités habituelles de la vie de tous les jours. Même chez les éleveurs, un seul berger ne devait guère dépasser ce nombre pour son propre troupeau … La norme de rentabilité pour un éleveur bio, qui transforme son lait, aujourd’hui encore, c’est soixante bêtes. Cette limite lexicale des nombres a fait prendre au « peuple », au Moyen-âge, des initiatives malheureuses pour nommer les nouveaux nombres qui apparaissaient avec le système décimal. Bien évidemment, dans la lutte entre les abacistes (les lettrés latinistes et l’Eglise) et les algoristes (les marchands, les notaires et le peuple) chacun suivait sa voie. Ces derniers avec soixante-dix (soixante et encore dix) ont réutilisé la construction latine du système additif romain). Quatre-vingt est encore plus primaire, c’est quatre fois les doigts des pieds et des mains, comme le peuple racine des papous en Nouvelle Guinée, actuellement. Dans ce cas, « le peuple » n’a pas fait preuve de beaucoup d’esprit scientifique. Enfin le bouquet final, c’est quatre-vingt-dix (quatre fois les orteils et les doigts des mains et encore dix avec le retour au système additif romain). Là on est dans le ridicule 5 …
-
L’abstraction pure, la route de l’enfer,
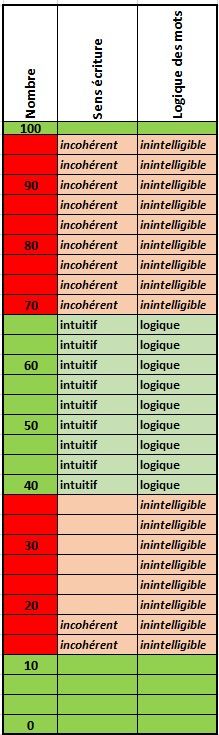
Ce système de numération caractérisé par l’utilisation d’une liste de « mots-nombres », d’expressions-nombres, irréguliers et illogiques pour plus d’un sur deux, ne peut être apprise que comme un poème dont le sens nous échappe, c’est-à-dire, « par cœur ». En maternelle, c’est l’objectif de la comptine. C’est cette comptine dans la numération conventionnelle, comme premier apprentissage mathématique, en l’absence du nombre-quantité, qui va fabriquer des écoliers en difficulté (figure 4). Aucune image technique n’est envisageable ; nous avons affaire à des « abstractions pures » et non pas à des « abstractions empiriques ».
Comment oser faire perdurer et enseigner un tel fatras d’absurdités archaïques, depuis des siècles, et des siècles ? Mais, aujourd’hui, la sanction est tombée. L’outil de mesure international de l’efficacité dans l’apprentissage des mathématiques à 10 ans en CM1 est disponible ce qui n’était pas le cas, pour la France, il y a seulement vingt-cinq ans (Pisa est arrivé en 2000 et Timss en 2015). Pour nommer les nombres, toutes les autres langues du monde sont totalement logiques y compris les langues vernaculaires. Les très rares exceptions (ce sont bien des exceptions) touchent les langues anglo-saxonnes (deux) et hispaniques (cinq). En Français l’illogisme et l’incohérence sont la règle (cinquante-six, de ce qu’on ne peut plus appeler des exceptions).
Après Timss 2015, 2019, Timss 2023, ne nous leurrons pas, Timss 2027 et Timss 2035 donneront un classement identique où la France se retrouvera dans le groupe des pays en voie de développement (Monténégro, Kazakhstan, etc.) derrière tous les pays développés.
5 La France est la risée du monde entier « Heureusement que le Ridicule ne tue pas sinon nous devrions annoncer 350 Millions de victimes francophones (illustration par un taxi Newyorkais, de notre « façon de compter » absurde, en Français
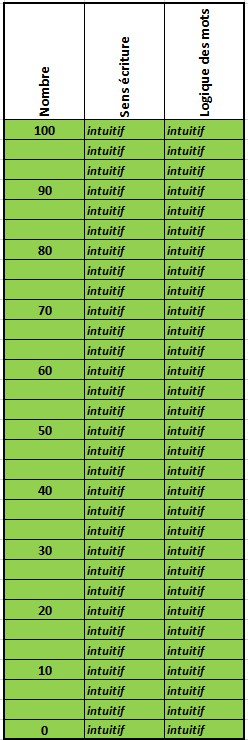
Figure 4 Le système conventionnel et le système Révolutionnaire de Condorcet
3/ De la Numération, les conséquences du choix de la mauvaise voie d’apprentissage, la Numération conventionnelle archaïque
Sans réforme de cet apprentissage la catastrophe à l’école primaire va perdurer longtemps. On peut, comme nous l’avons déjà vu, pronostiquer des classements encore rédhibitoires pour les classements TIMSS 2027, 2031 et 2035, des élèves de CM1 à 10 ans, compte tenu de l’éventuelle étude de l’Agence Nationale de la Recherche (quatre années). L’État est informé officiellement depuis 2020 et formellement depuis le 09 décembre 2024 pour le CNESCO par lettre RAR et le Ministère le 11 janvier 2025, par une lettre à madame la Ministre, Les conséquences directes de ce retard dans les décisions de l’État sont :
-
Laisser en souffrance au moins un tiers des enfants en primaire et, en suivant au collège, où les difficultés touchent près de 50 % des élèves. Le Ministère le reconnaît 6 dans sa Note Lecture : « 67,1 % des élèves répondant en 2019 déclarent être « D’accords » ou « Tout à fait d’accords » avec l’affirmation « Je fais des mathématiques parce que cela me plaît », contre 75,8 % en 2014 ». Un antonyme de plaisir est « souffrance » ou « douleur ». Et là, les enseignants sont d’accords pour parler de 50 % dès le CP. Retenons le taux minimal (100 – 67,1 %, soit 32,9 %) de la DEPP. Les familles peuvent constater que ce désamour des maths s’étend, ensuite à l’école en général.
-
Dans les mesures faites par l’enquête Timss 2023,
Voici les scores moyens de la France :
6 Note d’information n°20.33 © DEPP

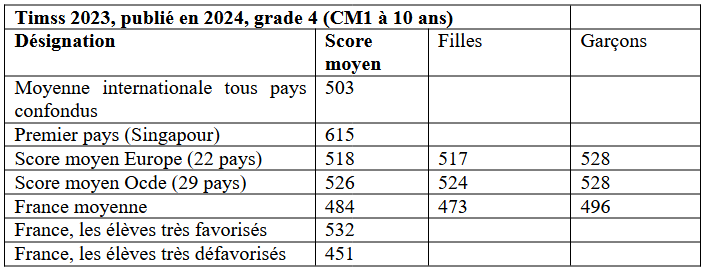
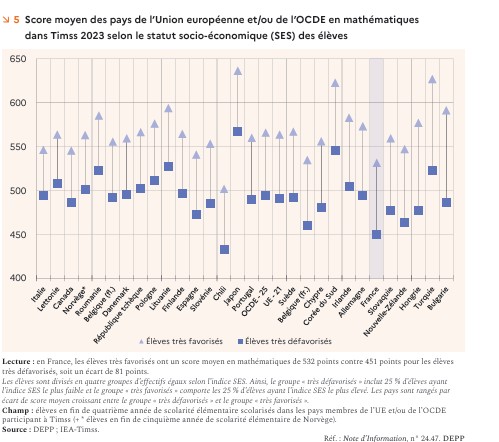
c) Les difficultés et le retard par rapport aux pays étrangers touchent tous les élèves y compris ceux qui sont privilégiés ; avec un score de 532, ils se retrouvent derrière tous les autres pays hormis le Chili. Les élèves d’origine sociale modeste, avant derniers, aussi, avec un score de 451, sont en outre pénalisés moralement par la conséquence de l’écart existant entre les deux populations, écart qui est un des plus importants du monde. Comment ces enfants défavorisés vivent-ils cette réussite inégale dans les mêmes classes ? Comme nous l’explique Bourdieu, le système retient dans les évaluations les élèves qui réussissent et néglige les autres comme si leur échec en était un corollaire inéluctable. Ces derniers sont stigmatisés et souffrent.
d) Comment les enfants originaires de familles d’immigrations récentes, slaves, asiatiques, et arabes notamment, vivent-ils le passage d’une numération, apprise en famille avec la langue de leurs origines, qui est parfaitement logique vers une numération française incompréhensible ? Ils sont perturbés et leur première impression de l’école française est très, très négative.
Nous avons ainsi, assez d’arguments pour expliquer la désaffection pour les mathématiques et ensuite le rejet de l’école de ces enfants stigmatisés, rejet qui va les conduire jusqu’à vandaliser, à seulement 10 ou 11 ans, les écoles de la République. C’est dire leurs ressentiments … Certains pensent que ces enfants laissés pour compte, parias du système, risquent en grandissant de rendre crédible les avertissements de divers chercheurs ou politologues 7 qui craignent une révolution ou une guerre civile dans notre pays.
7 David Betz du King’s ‘Collège de Londres ; William Thay, Think Tank « Le Millénaire »,
4/ De la Numération, comment l’État gère la situation issue de l’apprentissage de notre Numération conventionnelle archaïque
a) Notre aveuglement, en France, est collectif mais l’ensemble de la population mondiale connait les originalités absurdes de notre système de numération et s’en gausse.
Le pays est mis au ban de toutes les nations, critiqué par n’importe quelle personne sur terre qui a entendu une seule fois compter en français.
b) L’État français se comporte exactement comme le décrivait Bourdieu : « la classe dirigeante, qui tient en main l’État, perpétue ce pouvoir par un moyen de force, l’Éducation. C’est un pouvoir de violence symbolique » conformément au schéma de Bourdieu (figure 5). L’Immobilisme prévaut au détriment des classes sociales défavorisées en difficulté, qui se voient ainsi empêchées de prendre l’ascenseur social. L’utilisation de la Numération de Condorcet résoudrait le problème immédiatement en proposant une système intuitif accessible à tous sans effort aucun, en parallèle de la numération conventionnelle. Au lieu de cela, la difficulté du système élimine d’office les plus faibles.
c) L’État désinforme à tout-va pour cacher la vérité.
- Un commentaire juste (figure 1), « la stabilité » attire l’attention mais cette stabilité aurait dû être qualifiée ainsi « à un niveau catastrophique » pour approcher la réalité.
- Le rédacteur apporte un autre élément pour crédibiliser les écrits de la DEPP, « les résultats sont sous la moyenne européenne ». On se dit « bel effort d’honnêteté » ! En réalité la France est le dernier pays européen et donc forcément en dessous de la moyenne puisque dernier.
- Le rédacteur poursuit : « hausse des inégalités entre filles et garçons ». Enfin une information intéressante, mais c’est une information secondaire destinée à cacher l’information principale qui aurait due être mise en valeur : notre classement est indicible. Au 42ème rang sur 58 pays avec un score de 484, nous sommes au ban des nations développés. Il n’y a qu’à lire la liste des pays classés après nous pour prendre conscience de la catastrophe.
- Madame la ministre de l’ÉN a même, cité un détail technique du programme mathématique, pour expliquer notre classement rédhibitoire : ce serait la faute aux « fractions » qui devraient être enseignés dès le CP et seraient la cause de notre retard. C’est ubuesque mais, surtout, c’est un point de détail qui, mis en avant, va dans le sens des lecteurs-auditeurs pour qui les fractions conservent un aspect rébarbatif. Nous savons tous que les fractions sont en fait une représentation d’une situation de proportionnalité et sont accessibles dès la GS, à l’occasion de « la fabrication du gâteau au yahourt ». Cela détourne l’attention, fait peur aux « non matheux » et permet de ne pas parler des vrais problèmes.
- Dans les résultats de Timss 2023, à l’âge de 10 ans, selon l’indice SES, l’écart entre le groupe des 25 % les plus défavorisés et celui des 25% les plus favorisés, est un des plus importants du monde. Cette information devrait inciter nos dirigeants à rechercher un facteur culturel et de technique didactique généralisée qui serait à l’origine de cet étirement entre les extrêmes des origines sociales, score de 451 contre 532, soit un écart de 81 points. Ceci, d’autant plus, que la Belgique Wallonne au contraire de la Belgique Flamande est dans la même situation que nous (une preuve de plus) au classement général et au classement des écarts sociaux. Insister sur cette dilatation de l’écart cache aussi la « vraie vérité » : les écoliers les plus favorisés, au même titre que les moins favorisés, se trouvent au dernier rang des pays de l’OCDE (hors Chili), donc un classement rédhibitoire pour l’ensemble des écoliers. Cette situation en elle-même, est une catastrophe absolue. Le classement confirme le retard de l’école française que nous situons à deux années environ par rapport à tous les pays étrangers, dont le Monténégro et le Kazakhstan. Nous avons déjà démontré que la formation et le professionnalisme des enseignants, ainsi que le budget alloué, n’était pas en cause.
- Cette situation en mathématiques est une mise au ban des nations. Comment un pays, au niveau du Monténégro, peut-il parler dans le concert des nations avec la voix que l’on peut attendre de la France ?
5/ De la Numération, la bonne voie d’apprentissage grâce à la Numération Révolutionnaire de Condorcet,
La Numération de Condorcet, n’a pas besoin d’argumentations en sa faveur (figure 4). Pour nommer les nombres, c’est l’équivalent logique qui existe dans toutes les autres langues du monde y compris les langues vernaculaires. L’apprentissage et l’appropriation de la numération par les enfants s’effectue de façon fluide et intuitive en quelques minutes, ou en quelques heures si l’on veut répondre au protocole d’évaluation de l’ÉN, inscrit dans les programmes du cycle 2, et valider ce savoir-faire. L’École de la République obtient le même résultat en deux ans minimum. Certains enseignants parlent même de trois ans, et pour certains enfants les difficultés vont perdurer jusqu’à l’âge adulte. Deux ans de perdu, au moins, qui pourraient être utilisés pour les différents autres apprentissages introduits dans les programmes officiels, dont les différentes matières submergent les enseignants.
L’Immobilisme habituel de la nation française devant les réformes ne va pas permettre un changement radical de système. Nous demandons, donc :
-
La vérification par un laboratoire universitaire et par l’ANR de notre découverte .
-
Une introduction à l’école de la Numération de Condorcet en apprentissage premier en CP de façon à « expliciter » la Numération Conventionnelle, sachant que le passage d’un système à l’autre, s’effectue, alors, et notre expérience le prouve, automatiquement, immédiatement et sans aucune perturbation chez des enfants qui ont, malgré tout, déjà la comptine en tête. Mais la logique est installée et l’enseignant peut s’appuyer sur elle pour la suite du programme avec les tables, les calculs, etc. qui seront étudiés en mode ‘mémoire procédurale’ et non grâce au « par cœur ». Les difficultés sont, alors, considérablement réduites.
Pas de réponse à ce jour à nos alertes de fin 2024 et début 2025

